Assigning Course Grades
I. Introduction
The end-of-course grades assigned by instructors are intended to convey the level of achievement of each student in the class. These grades are used by students, other faculty, university administrators, and prospective employers to make a multitude of different decisions. Unless instructors use generally-accepted policies and practices in assigning grades, these grades are apt to convey misinformation and lead the decision-maker astray. When grading policies and practices are carefully formulated and reviewed periodically, they can serve well the many purposes for which they are used.
What might a faculty member consider to establish sound grading policies and practices? The issues which contribute to making grading a controversial topic are primarily philosophical in nature. There are no research studies that can answer questions like: What should an "A" grade mean? What percent of the students in my class should receive a "C?" Should spelling and grammar be judged in assigning a grade to a paper? What should a course grade represent? These "should" questions require value judgments rather than an interpretation of research data; the answer to each will vary from instructor to instructor. But all instructors must ask similar questions and find acceptable answers to them in establishing their own grading policies. It is not sufficient to have some method of assigning grades--the method used must be defensible by the user in terms of his or her beliefs about the goals of an American college education and tempered by the realities of the setting in which grades are given. An instructor's view of the role of a university education consciously or unwittingly affects grading plans. The instructor who believes that the end product of a university education should be a "prestigious" group which has survived four or more years of culling and sorting has different grading policies from the instructor who believes that most college-aged youths should be able to earn a college degree in four or more years.
An instructor's beliefs are influenced by many factors. As any of these factors change there may be a corresponding change in belief. The type of instructional strategy used in teaching dictates, to some extent, the type of grading procedures to use. For example, a mastery learning approach1 to teaching is incongruent with a grading approach which is based on competition for an arbitrarily set number of "A" or "B" grades. Grading policies of the department, college, or campus may limit the procedures which can be used and force a basic grading plan on each instructor in that administrative unit. The recent response to grade inflation has caused some faculty, individually and collectively, to alter their philosophies and procedures. Pressure from colleagues to give lower or higher grades often causes some faculty members to operate in conflict with their own views. Student grade expectations and the need for positive student evaluations of instruction probably both contribute to the shaping or altering of the grading philosophies of some faculty. The dissonance created by institutional restraints probably contributes to the wide-spread feeling that end-of-course grading is one of the least pleasant tasks facing a college instructor.
With careful thought and periodic review, most instructors can develop satisfactory, defensible grading policies and procedures. To this end, several of the key issues associated with grading are identified in the sections which follow. In each case, alternative viewpoints are described and advantages and disadvantages noted. Regulations pertaining to grading at the University of Illinois are presented in Article 3, Part 1 of the Student Code.
1Airasian, P. W., Block, J. H., Bloom, B. S., & Carroll, J. B., (1971) Mastery learning: Theory and practice (J. Block, Ed.). Holt, Rinehart & Winston.
II. Grading Comparisons
Some kind of comparison is being made when grades are assigned. For example, an instructor may compare a student's performance to that of his or her classmates, to standards of excellence (i.e., pre-determined objectives, contracts, professional standards) or to combinations of each. Four common comparisons used to determine college and university grades and the major advantages and disadvantages of each are discussed in the following section.
Comparisons With Other Students
By comparing a student's overall course performance with that of some relevant group of students, the instructor assigns a grade to show the student's level of achievement or standing within that group. An "A" might not represent excellence in attainment of knowledge and skill if the reference group as a whole is somewhat inept. All students enrolled in a course during a given semester or all students enrolled in a course since its inception are examples of possible comparison groups. The nature of the reference group used is the key to interpreting grades based on comparisons with other students.
Some Advantages of Grading Based on Comparison With Other Students
- Individuals whose academic performance is outstanding in comparison to their peers are rewarded.
- The system is a common one that many faculty members are familiar with. Given additional information about the students, instructor, or college department, grades from the system can be interpreted easily.
Some Disadvantages of Grading Based on Comparison With Other Students
- No matter how outstanding the reference group of students is, some will receive low grades; no matter how low the overall achievement in the reference group, some students will receive high grades. Grades are difficult to interpret without additional information about the overall quality of the group.
- Grading standards in a course tend to fluctuate with the quality of each class of students. Standards are raised by the performance of a bright class and lowered by the performance of a less able group of students. Often a student's grade depends on who was in the class.
- There is usually a need to develop course "norms" which account for more than a single class performance. Students of an instructor who is new to the course may be at a particular disadvantage since the reference group will necessarily be small and very possibly atypical compared with future classes.
Comparisons with Established Standards
Grades may be obtained by comparing a student's performance with specified absolute standards rather than with such relative standards as the work of other students. In this grading method, the instructor is interested in indicating how much of a set of tasks or ideas a student knows, rather than how many other students have mastered more or less of that domain. A "C" in an introductory statistics class might indicate that the student has minimal knowledge of descriptive and inferential statistics. A much higher achievement level would be required for an "A." Note that students' grades depend on their level of content mastery; thus the levels of performance of their classmates has no bearing on the final course grade. There are no quotas in each grade category. It is possible in a given class that all students could receive an "A" or a "B."
Some Advantages of Grading Based on Comparison to Absolute Standards
- Course goals and standards must necessarily be defined clearly and communicated to the students.
- Most students, if they work hard enough and receive adequate instruction, can obtain high grades. The focus is on achieving course goals, not on competing for a grade.
- Final course grades reflect achievement of course goals. The grade indicates "what" a student knows rather than how well he or she has performed relative to the reference group.
- Students do not jeopardize their own grade if they help another student with course work.
Some Disadvantages of Grading Based on Comparison to Absolute Standards
- It is difficult and time consuming to determine what course standards should be for each possible course grade issued.
- The instructor has to decide on reasonable expectations of students and necessary prerequisite knowledge for subsequent courses. Inexperienced instructors may be at a disadvantage in making these assessments.
- A complete interpretation of the meaning of a course grade cannot be made unless the major course goals are also available.
Comparisons Based on Learning Relative to Improvement and Ability
The following two comparisons—with improvement and ability—are sometimes used by instructors in grading students. There are such serious philosophical and methodological problems related to these comparisons that their use is highly questionable for most educational situations.
Relative to Improvement...
Students' grades may be based on the knowledge and skill they possess at the end of a course compared to their level of achievement at the beginning of the course. Large gains are assigned high grades and small gains are represented by low grades. Students who enter a course with some pre-course knowledge are obviously penalized; they have less to gain from a course than does a relatively naive student. The post test–pretest gain score is more error-laden, from a measurement perspective, than either of the scores from which it is derived. Though growth is certainly important when assessing the impact of instruction, it is less useful as a basis for determining course grades than end-of-course competence. The value of grades which reflect growth in a college-level course is probably minimal.
Relative to Ability...
Course grades might represent the amount students learned in a course relative to how much they could be expected to learn as predicted from their measured academic ability. Students with high ability scores (e.g., scores on the SAT or ACT) would be expected to achieve higher final examination scores than those with lower ability scores. When grades are based on comparisons with predicted ability, an "overachiever" and an "underachiever" may receive the same grade in a particular course, yet their levels of competence with respect to the course content may be vastly different. The first student may not be prepared to take a more advanced course, but the second student may be. A course grade may, in part, reflect the amount of effort the instructor believes a student has put into a course. The high ability students who can satisfy course requirements with minimal effort are penalized for their apparent "lack" of effort. Since the letter grade alone does not communicate such information, the value of ability-based grading does not warrant its use.
A single course grade should represent only one of the several grading comparisons noted above. To expect a course grade to reflect more than one of these comparisons is too much of a communication burden. Instructors who wish to communicate more than relative group standing, or subject matter competence or level of effort, must find additional ways to provide such information to each student. Suggestions for doing so are noted near the end of Section V.
III. Basic Grading Guidelines
1. Grades Should Conform to the Practice in the Department and the Institution in Which the Grading Occurs.
Grading policies of the department, college, or campus may limit the grading procedures which can be used and force a basic grading philosophy on each instructor in that administrative unit. Departments often have written statements which specify a method of assigning grades and meanings of grades. If such grading policies are not explicitly stated or written for faculty use, the percentages of A's, B's, C's, D's, and F's given by departments and colleges in their 100-level, 200- level, 300-level and graduate courses may be indicative of implicitly stated grading policies. Grade distribution information is available from all departmental offices or from Measurement and Evaluation (M&E) of the Center for Innovation in Teaching and Learning (CITL).
The University regulations encourage a uniform grading policy so that a grade of A, B, C, D, or F will have the same meaning independent of the college or department awarding the grade. In practice grade distributions vary by department, by college, and over time within each of these units. The grading standards of a department or college are usually known by other campus units. For example, a "B" in a required course given by Department X might indicate that the student probably is not a qualified candidate for graduate school in that or a related field. Or, a "B" in a required course given by Department Y might indicate that the student's knowledge is probably adequate for the next course. Grades in certain "key" courses may also be interpreted as a sign of a student's ability to continue work in the field. The faculty member who is uninformed about the grading grapevine may unwittingly make misleading statements about a student and also misinterpret information received. If an instructor's grading pattern differs markedly from others in the department or college and the grading is not being done in special classes (e.g., honors, remedial), the instructor should reexamine his or her grading practices to see that they are rational and defensible. Sometimes an individual faculty member's grading policy will differ markedly from that of the department and/or college and yet be defensible. For example, the department and instructor may be using different grading standards, course structure may seem to require a grading plan which differs from departmental guidelines, or the instructor and department may hold different ideas about the function of grading. Usually in such cases, a satisfactory grading plan can be worked out. Faculty new to the University can consult with the department head for advice about grade assignment procedures in particular courses. Measurement and Evaluation will consult with faculty on grading problems and procedures.
2. Grading Components Should Yield Accurate Information.
Carefully written tests and/or graded assignments (homework papers, projects) are keys to accurate grading. Because it is not customary at the university level to accumulate many grades per student, each grade carries great weight and should be as accurate as possible. Poorly planned tests and assignments increase the likelihood that grades will be based primarily on factors of chance. Some faculty members argue that over the course of a college education, students will receive an equal number of higher-grades-than-merited and lower-grades-than-merited. Consequently, final GPA's will be relatively correct. However, in view of the many ways course grades are used, each course grade is often significant in itself to the student and others. No evaluation efforts can be expected to be perfectly accurate, but there is merit in striving to assign course grades that most accurately reflect the level of competence of each student.
3. Grading Plans Should Be Communicated to the Class at the Beginning of Each Semester.
By stating the grading procedures at the beginning of a course, the instructor is essentially making a "contract" with the class about how each student is going to be evaluated. The contract should provide the students with a clear understanding of the instructor's expectations so that the students can structure their work efforts. Students should be informed about: which course activities will be considered in their final grade; the importance or weight of exams, quizzes, homework sets, papers and projects; and which topics are more important than others. Students also need to know what method will be used to assign their course grade and what kind of comparison the course grade will represent. By informing students early in the semester about course priorities, the instructor encourages students to study what he or she deems valuable. All of this information can be communicated effectively as a part of the course outline or syllabus.
4. Grading Plans Stated at the Beginning of the Course Should Not Be Changed Without Thoughtful Consideration and a Complete Explanation to the Students.
Two common complaints found on students' post-course evaluations are that grading procedures stated at the beginning of the course were either inconsistently followed or were changed without explanation or even advanced notice. One could look at the situation of altering or inconsistently following the grading plan as being analogous to playing a game wherein the rules arbitrarily change, sometimes without the players' knowledge. The ability to participate becomes an extremely difficult and frustrating experience. Students are placed in the unreasonable position of never knowing for sure what the instructor considers important. When the rules need to be changed all of the players must be informed (and hopefully be in agreement).
5. The Number of Components or Elements Used to Assign Course Grades Should Be Large Enough to Enhance High Accuracy in Grading.
From a decision-making point of view, the more pieces of information available to the decision-maker, the more confidence one can have that the decision will be accurate and appropriate. This same principle applies to the process of assigning grades. If only a final exam score is used to assign a course grade, the adequacy of the grade will depend on how well the test covered all the relevant aspects of course content and how typically the student performed on one specific day during a 2-3 hour period. Though the minimum number of tests, quizzes, papers, projects, and/or presentations needed must be course- specific, each instructor must attempt to secure as much relevant data as are reasonably possible to ensure that the course grade will accurately reflect each student's achievement level.
IV. Some Methods of Assigning Course Grades
Various grading practices are used by college and university faculty. Following is an examination of the more widely used methods and discussion of the advantages, disadvantages and fallacies associated with each.
Weighting Grading Components and Combining Them to Obtain a Final Grade
Grades are typically based on a number of graded components (e.g., exams, papers, projects, quizzes). Instructors often wish to weight some components more heavily than others. For example, four combined quiz scores may be valued at the same weight as each of four hourly exam grades. When assigning weights the instructor should consider the extent to which:
- each grading component measures important goals.
- achievement can be accurately measured with each grading component.
- each grading component measures a different area of course content or objectives compared to other components.
Once it has been decided what weight each grading component should have, the instructor should ensure that the desired weights are actually used. This task is not as simple as it first appears. An extreme example of weighting will illustrate the problem.
Suppose that a 40-item exam and an 80-item exam are to be combined so they have equal weight (50 percent-50 percent in the total). We must know something about the spread of scores or variability (e.g., standard deviation) on each exam before adding the scores together. For example, assume that scores on the shorter exam are quite evenly spread throughout the range 10-40, and the scores on the other are in the range 75-80. Because there is so little variability on the 80-item exam, if we merely add each student's scores together, the spread of scores in the total will be very much like the spread of scores observed on the first exam. The second exam will have very little weight in the total score. The net effect is like adding a constant value to each student's score on the 40-item exam; the students maintain essentially the same relative standing.
| Exam No. 1 | Exam No. 2 | Total | |
|---|---|---|---|
| Number of items | 40 | 80 | 120 |
| Standard deviation | 7.0 | 3.5 | |
| Desired weight | 1 | 1 | |
| Observed weight | 2 | 1 | |
| Multiplying factor | 1 | 2 | |
| New standard deviation | 7.0 | 7.0 | |
| Actual weight | 1 | 1 |
The information appearing in Figure 1 will be used to demonstrate how scores can be adjusted to achieve the desired weighting before combining them. Exam No. 2 is twice as long as the first, but there is twice as much variability in Exam No. 1 scores. (This is the "observed weight.") The standard deviation tells us, conceptually, the average amount by which scores deviate from the mean of test scores. The larger the value, the more the scores are spread throughout the possible range of test scores. The variability of scores (standard deviation) is the key to proper weighting. If we merely add these scores together, Exam No. 1 will carry 66 percent of the weight and Exam No. 2 will carry 33 percent weight. We must adjust the scores on the second exam so that the standard deviation of the scores will be similar to that for Exam No. 1. This can be accomplished by multiplying each score on the 80-item exam by two; the adjusted scores will become more varied (standard deviation = 7.0). The score from Exam No. 1 can then be added to the adjusted score from Exam No. 2 to yield a total in which the components are equally weighted. (A practical solution to combining several weighted components is to first transform raw scores to standard scores, z or T, before applying relative weights and adding.) Additional reading can be found in Ebel & Frisbie (1991); Linn & Gronlund (1995); and Ory & Ryan (1993).
After grading weights have been assigned and combined scores are calculated for each student, the instructor must change the numbered scores into one of five letter grades. There are several ways of doing this; some are more appropriate than others.
The Distribution Gap Method
This widely-used method of assigning test or course grades is based on the relative ranking of students in the form of a frequency distribution or tally of student exam scores. The frequency distribution is carefully scrutinized for gaps, several consecutive scores which have zero frequency. A horizontal line is drawn at the top of the first gap ("Here are the A's") and a second gap is sought. The process continues until all possible grade ranges (A-F) are identified. The major fallacy with this technique is the dependence on "chance" to form the gaps. The gaps are random because measurement errors (due to guessing, poorly written items, etc.) dictate where gaps will or will not appear. If scores from an equivalent test could be obtained from the same group, the gaps would likely appear in different places. Some students would get higher grades, some would get lower grades, and many grades would remain unchanged. Unless the instructor has additional achievement data to reevaluate borderline cases, many students could see their fate determined more by chance than performance.
Grading on the Curve
This method of assigning grades based on group comparisons is complicated by the need to establish arbitrary quotas for each grade category. What percent should get A's? B's? D's? Once these quotas are fixed, grades are assigned without regard to level of performance. The highest ten percent may have achieved at about the same level. Those who "set the curve" or "blow the top off the curve" are merely among the top group; their grade may be the same as that of a student who scored 20 points lower. The bottom five percent may be assigned F's though the bottom fifteen percent may be relatively indistinguishable in achievement. Quota-setting strategies vary from instructor to instructor and department to department and seldom carry a defensible rationale. While some instructors defend the use of the normal or bell shaped curve as an appropriate model for setting quotas, using the normal curve is as arbitrary as using any other curve. It is highly unlikely that our college and university student abilities or achievement are normally distributed. Grading on the curve is efficient from an instructor point of view. Therein lies the only merit in the method.
Percent Grading
The long-standing use of percent grading in any form is questionable. Scores on papers, tests, and projects are typically converted to a percent based on the total possible score. The percent score is then interpreted as the percent of content, skills or knowledge over which the student has command. Thus an exam score of 83 percent means that the student knows 83 percent of the content which is represented by the test items. Grades are usually assigned to percent scores using arbitrary standards similar to those set for grading on the curve, i.e., students with scores 93-100 get A's and 85-92 is a B, 78-84 is a C, etc. The restriction here is on the score ranges rather than on the number of individuals who can earn each grade. Should the cutoff for an A be 92 instead? Why not 90? What sound rationale can be given for any particular cutoff? In addition, it seems indefensible in most cases to set grade cutoffs that remain constant throughout the course and several consecutive offerings of the course. It does seem defensible for the instructor to decide on cutoffs for each grading component, independent of the others, so that the scale for an A might be 93-100 for Exam No. 1, 88-100 for a paper, 87-100 for Exam No. 2 and 90-100 for the Final Exam. Some instructors who use percent grading find themselves in a bind when the highest score obtained on an exam is only 68 percent, for example. Was the examination much too difficult? Did students study too little? Was instruction relatively ineffective? Oftentimes, instructors decide to "adjust" scores so that 68 percent is equated to 100 percent. Though the adjustment might cause all concerned to breathe easier, the new score is essentially the percentage of exam content learned by the students. The exam score of 83 no longer means that the student knew 83 percent of the exam content.
A Relative Grading Method
Using group comparisons for grading is appropriate when the class size is sufficiently large (perhaps 35 students or more) to provide a reference group representative of students typically enrolled in the course. The following steps describe a widely used and generally sound procedure:
- Convert raw scores on each exam to a standard score (z or T) by using the mean and standard deviations from each respective test, set of papers, or presentations (see Appendix). Standard scores are recommended because they allow us to measure performance on each grading component with an identical or standard yardstick. When relative comparisons are to be made, it is not advisable to convert raw scores to grades and average the separate grades. This is because the distinction between achievement levels will be lost; differences will melt together as students are forced into a few broad categories.
- Weight each grading variable before combining the standard scores. For example, double both exam standard scores and the standard score for the paper, triple the final exam standard score, and do nothing to the standard score for the presentation. The respective weights for these variables in the total will then be 20 percent, 20 percent, 20 percent, 30 percent, and 10 percent.
- Add these weighted scores to get a composite or total score.
- Build a frequency distribution of the total scores by listing all obtainable scores and the number of students receiving each. Calculate the mean, median, and standard deviation (see Appendix). Most calculators now available will perform these operations quickly.
- If the mean and median are similar in value, use the mean for further computations. Otherwise use the median. Let's assume we have chosen the median. Add one half of the standard deviation to the median and subtract the same value from the median. These are the cutoff points for the range of C's.
- Add one standard deviation to the upper cutoff of the C's to find the A-B cutoff. Subtract the same value from the lower cutoff of the C's to find the D-F cutoff.
- Use number of assignments complete or quality of assignments or other relative achievement data available to reevaluate borderline cases. Measurement error exists in composite scores too!
Instructors will need to decide logically on the values to be used for finding grade cutoffs (one-half, one-third, or three-fourths of a standard deviation, for example). How the current class compares to past classes in ability should be judged in setting standards. When B rather than C is considered the average grade, step five will identify the A-B and C-B cutoffs. Step six would be changed accordingly.
Relative grading methods like the one outlined above are not free from limitations; subjectivity enters into several aspects of the process. But a systematic approach similar to this one, and one which is thoroughly described in the first class meeting, is not likely to be subject to charges of capricious grading and miscommunication between student and instructor.
An Absolute Standard Grading Method
Absolute grading is the only form of assigning grades which is compatible with mastery or near-mastery teaching and learning strategies. The instructor must be able to describe learner behaviors expected at the end of instruction so that grading components can be determined and measures can be built to evaluate performance. Objectives of instruction are provided for students to guide their learning, and achievement measures (tests, papers, and projects) are designed from the sets of objectives.
Each time achievement is measured, the score is compared with some criterion or standard set by the instructor. Students who do not meet the minimum criterion level study further, rewrite their paper, or make changes in their project to prepare to be evaluated again. This process continues until the student meets the minimum standards established by the instructor. The standards are an important key to the success of this grading method. The following example illustrates how the procedures can be implemented step-by-step:
- Assume that a test has been built using the objectives from two units of instruction. Read each test item and decide if a student with minimum mastery could answer it correctly. For short answer or essay items, decide how much of the ideal answer the student must supply to demonstrate minimum mastery. Make subjective decisions, in part, on the basis of whether or not the item measures important prerequisites for subsequent units in the course or subsequent courses in the students' programs of study.
- The sum of the points from the above step represents the minimum score for mastery. Next, decide what grade the criterion score should be associated with. (Assume for our purposes that the criterion represents the C-B cutoff.)
- Reexamine items which students are not necessarily expected to answer correctly to show minimum mastery. Decide how many of these items "A" students should answer correctly. Such students would exhibit exceptionally good preparation for later instruction. (This step could be done concurrently with Step 1.)
- Add the totals from Steps 1 and 3 to find the criterion score for the B-A grade cutoff.
- Each criterion score set in the above fashion should be adjusted downward by 2-4 points. This adjustment takes measurement error into account. It 16. compensates for the fact that as test constructors, we may write a few ambiguous or highly difficult items which a well-prepared student might miss due to our own inadequacies.
- After the exam has been scored, assign "A," "B," and "C or less" grades using the criterion scores. Students who earn "C or less" should be given a different but equivalent form of the test within two weeks. A criterion score must be set for this test as described in Step 1. Students who score above the criterion can earn a "B" at most. Those who fail to meet the criterion on the second testing might be examined orally by the instructor for subsequent checks on their mastery.
- Weight the grades from the separate exams, papers, presentations, and projects according to the percentages established at the outset of the course. Average the weighted grades (using numerical equivalents, e.g., A = 5, B = 4, etc.) to determine the course grade. Borderline cases can be reexamined using additional achievement data from the course.
V. GRADING VS. EVALUATION
A distinction should be made between components which an instructor evaluates and components which are used to determine course grades. Components or variables which contribute to determining course grades should reflect each student's competence in the course content. The components of a grade should be academically oriented—they should not be tools of discipline or awards for pleasant personalities or "good" attitudes. A student who gets an "A" in a course should have a firm grasp of the skills and knowledge taught in that course. If the student is merely marginal academically but very industrious and congenial, an "A" grade would be misleading and would render a blow to the motivation of the excellent students in the program. Instructors can give feedback to students on many traits or characteristics, but only academic performance components should be used in determining course grades.
Some potentially invalid grading components are considered below. Though some exceptions could be noted, these variables generally should not be used to determine course grades.
Class Attendance
Students should be encouraged to attend class meetings because it is assumed that the lectures, demonstrations, and discussion will facilitate their learning. If students miss several classes then their performance on examinations, papers, and projects will likely suffer. If the instructor further reduces the course grade because of absence, the instructor is essentially submitting such students to "double jeopardy." For example, an instructor may say that attendance counts ten percent of the course grade, but for students who are absent frequently this may in effect amount to 20 percent. Teachers who experience a good deal of class "cutting" might examine their classroom environment and methods to determine if changes are needed and ask their students why attendance was low.
Class Participation
Obviously seminars and small classes depend on student participation to some degree for their success. When participation is important, it may be appropriate for the instructor to use participation grades. In such cases the instructor should keep weekly notes regarding frequency and quality of participation; waiting until the end of the semester and relying strictly on memory makes a relatively subjective task even more subjective. Participation should probably not be graded in most courses, however. Dominating or extroverted students tend to win and introverted or shy students tend to lose. Students should be graded in terms of their achievement level, not in terms of their personality type. Instructors may want to give feedback to students on many aspects of their personality but grading should not be the means of doing so.
Mechanics
Neatness is written work, correctness in spelling and grammar, and organizational ability are all worthy traits. They are assets in most vocational endeavors. To this extent it seems appropriate that instructors evaluate these factors and give students feedback about them. However, unless the course objectives include instruction in these skills, students should not be graded on them in the course. A student's grade on an essay exam should not be influenced by his/her general spelling ability, neither should his/her course grade.
Personality Factors
Most instructors are attracted to students who are agreeable, friendly, industrious, and kind; we tend to be repelled by those with opposite characteristics. To the extent that certain personalities may interfere with class work or have limited chances for employment in their field of interest, constructive feedback from the instructor may be necessary. An argumentative student who earns a "C" should have a moderate amount of knowledge about the course content. The nature of his or her personality should not have direct bearing on the course grade earned.
Instructors can and should evaluate many aspects of student performance in their course. However, only the evaluation information which relates to course goals should be used to assign a course grade. Judgments about writing and speaking skills, personality traits, effort, and motivation should be communicated in some other form. Some faculty use brief conferences for this purpose. Others communicate through comments written on papers or through the use of mock letters of recommendation.
VI. GRADING IN MULTI-SECTIONED COURSES
Some rather unique grading problems are associated with large multiple-sectioned courses taught by many different instructors under the direction and leadership of one head instructor. In many of these situations there is a common course outline or syllabus, common text, and a set of common classroom tests. The head instructor is often concerned about the potential lack of equity in grading standards and practices across the many sections. To promote fairness and equality, the following conditions might be established as part of course planning and monitored throughout the semester by the head instructor:
- The number and type of grading components (e.g., papers, quizzes, exams) should be the same for each section.
- All grading components should be identical or nearly equivalent in terms of content measured and level of difficulty.
- Section instructors should agree on the grading standards to be used (e.g., cutoff scores for grading quizzes, papers, or projects; weights to be used with each component in formulating a semester total score; and the level of difficulty of test questions to be used).
- Evaluation procedures should be consistent across sections (e.g., method of assigning scores to essays, papers, lab write-ups, and presentations).
Though all of these conditions can be addressed in the course planning stage, their implementation may be a more difficult task. Successful implementation requires a spirit of compromise between section instructors and the head instructor as well as among section instructors. Frequent review of instructor practices by the head instructor and constructive feedback to the instructors are also needed. The following guidelines contain suggestions for promoting equity in grading across multiple sections:
- To establish common grading components in each course section, all section instructors should agree at the beginning of the course on the number and kind of components to be used. Agreement should also be reached on the component weighting scheme and final requirements for each course grade (A, B, C, etc.).
- To encourage instructional adequacy across sections, many head instructors distribute the same course objectives, outlines, lecture notes and handouts to all section instructors. If each instructor is allowed to contribute to the construction of common tests, quizzes, or projects, the section instructors will become more aware of important course content and the expectations of the head instructor. This awareness will serve to "standardize" section instruction, also.
- Prior to the administration of an exam, quiz or project, all instructors should agree on established letter grade cutoff scores. The group consensus helps to standardize the administration of grading procedures by reducing the number of "lone wolves" who wish not to conform to someone else's standards.
- In cases where the grading of particular components is more subjective than objective (e.g., more influenced by personal judgment), organized group practice helps to unify the application of evaluation procedures. For example, head instructors may wish to distribute examples of A, B, or C quality projects to section instructors as models prior to the grading of their own class projects. Or, groups of instructors may wish to practice grading a stack of essay exams by circulating and discussing their individual ratings. Through such group practice the instructors involved can compare their evaluation practices with one another and become more uniform over time.
- Any grading or evaluation changes made in a particular section should be implemented in all sections.
VII. EVALUATING GRADING POLICIES
- Instructors can compare their grade distributions with the grade distributions for similar courses in the same department. Information about grade distributions is available through individual departments or through Measurement and Evaluation of the Center for Innovation in Teaching and Learning.
EXAMPLE:
Suppose you taught one section of a 100-level course with 40 students. The course is the first in a three-course sequence which is required in the students' curriculum. Your grade distribution turned out to be:
A = 5% B = 20% C = 40% D = 30% F = 5%
When you compare your course grade distribution with that of all of the previous year's sections of the same course, you found the following grade distribution:
A = 22% B = 30% C = 38% D = 9% F = 1%
Because your grade distribution is not consistent with departmental practice, further investigation is warranted to find out if your particular class was atypical, if your expectations were too high, if the exams upon which the grades were based were too difficult for the course, etc. The fact that your grade distribution does not resemble the grades assigned by your colleagues does not necessarily indicate that your grading methods are incorrect or inappropriate. However, discrepancies that you regard as significant should suggest the need for reexamination of your grading practices in light of departmental or college policies.
- Students believe that fair and explicit grading policies are an important aspect of quality instruction. The following set of ICES (Instructor and Course Evaluation System) items can be used to obtain student perceptions of course grading. The items are presented with their original ICES catalog number*.
| # | Item | Left Anchor | Rating | Right Anchor |
|---|---|---|---|---|
| 101 | The grading procedures for the course were: | Very fair | 5-4-3-2-1 | Very unfair |
| 104 | Was the grading system for the course explained? | Yes, very well | 5-4-3-2-1 | No, not at all |
| 105 | Did the instructor have a realistic definition of excellent performance? | Yes, very realistic | 5-4-3-2-1 | No, very unrealistic |
| 106 | Did the instructor set too high/low grading standards for students? | Too high | 1-3-5-3-1 | Too low |
| 107 | How would you characterize the instructor's grading system? | Very objective | 5-4-3-2-1 | Very subjective |
| 108 | The amount of graded feedback given to me during the course was: | Quite adequate | 5-4-3-2-1 | Not enough |
| 110 | Were requests for re-grading or review handled fairly? | Yes, almost always | 5-4-3-2-1 | No, almost never |
| 111 | The instructor evaluated my work in a meaningful and conscientious manner | Strongly agree | 5-4-3-2-1 | Strongly disagree |
*For additional information about using the University of Illinois ICES System, call Measurement and Evaluation at 217-244-3846.
VIII. Assistance Offered by the Center for Innovation in Teaching and Learning (CITL)
Members of Measurement and Evaluation (M&E) and Instructional Development are well prepared to discuss course grading policies and procedures with faculty who wish to review or change their grading procedures. To inquire about these services email CITL at citl-info@illinois.edu.
IX. References for Further Reading
Dressel, P. L. (1961). Evaluation in higher education. Houghton Mifflin. 1961.
Ebel, R.L., & Frisbie, D.A. (1991). Essentials of educational measurement (5th ed.). Prentice-Hall.
Frisbie, D. A. (1977). Issues in formulating course grading policies. National association of colleges and teachers of agriculture journal, 21(4).
Frisbie, D. A. (1978). Methodological considerations in grading. National association of colleges and teachers of agriculture journal, 22(1).
Handlin, O., & Handlin, M. F. (1970). The American college and American culture: Socialization as a function of higher education. McGraw Hill.
Hill, J. R. (1976). Measurement and evaluation in the classroom. Merrill Publishing Co.
Linn, R., & Gronlund, N. (1995). Measurement and assessment in teaching (7th ed.). Prentice-Hall.
McKeachie, W. J. Teaching tips: A guidebook for the beginning college teacher (8th ed.). D. C. Heath and Co.
Mehrens, W. A. & Lehmann, I. J. (1973). Measurement and evaluation in education and psychology. Holt, Rinehart & Winston.
Ory, J. O., & Ryan, K. E. (1993). Writing and grading classroom examinations. Sage.
Terwilliger, J. S. (1971). Assigning grades to students. Scott, Foresman & Co.
X. Appendix
Test Statistics
- Mean
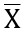 Score =
Score = 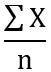 =
= 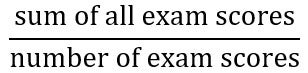
- where:
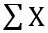 = sum of all X
= sum of all X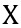 = an exam score
= an exam score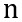 = number of exam scores
= number of exam scores
- where:
- Median (Mdn) Score = The 50th percentile of the score on either side of which half the scores occur.
- Standard Deviation (SD) =
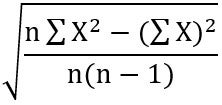
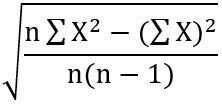
- where:
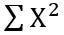 = sum of all squared exam scores
= sum of all squared exam scores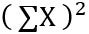 = squared sum of all exam scores
= squared sum of all exam scores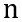 = number of exam scores
= number of exam scores
- NOTE: Many pocket calculators are programmed to compute standard deviations.
- where:
Standard Scores
- z-score =
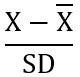
- where:
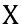 = an exam score
= an exam score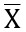 = mean score
= mean score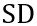 = standard deviation of exam
= standard deviation of exam
- where:
- T-Score = 50 + 10z
- The z- and T-score formulas serve the function of standardizing any exam score from any group of data by transforming the exam score to a score that has a constant meaning across all different sets of scores.
- The z-score identifies the number of standard deviation units that an exam score is above or below the class mean. Given a z-score of 0.5, one knows that the corresponding exam score was one half a standard deviation above the mean. Similarly, a z-score of -0.5 is one-half a standard deviation below the mean. A T-score is simply a converted z-score which has the decimal point and a negative sign removed. A T-score is computed by multiplying a z-score by ten and adding 50 to the result. Thus, a T-score of 60 represents an exam score that is one standard deviation above the mean, whereas a T-score of 40 is one standard deviation below the mean.
- Standard scores (z or T) provide information about a student's performance relative to the performance of the entire class. If one was told that Student A received an Exam score of 52, one cannot be sure how well that student performed in comparison to the rest of the class. However, the information that Student A obtained a z-score of +1.5 (T-score = 65) reveals that the performance was one and a half standard deviations above the class average, or rather high in comparison to the rest of the class.
- The exam analysis provided by Exam Services in CITL contains these statistics for exams administered with Scantrons.
